Question Reliability (Technical)

• Associated Instructional Materials:
  • Video: How To Know if an Assessment is Reliable

Question Reliability is a psychometric measure that quantifies the consistency and dependability of assessment questions within OnTarget. It indicates how reliably a set of questions measures the intended construct or subject area, with values ranging from 0 (least reliable) to 1 (most reliable).

Technical Interpretation

Reliability Scale

• Range: 0.0 to 1.0 (displayed as decimal values)
• 0.0: Questions show no consistency or reliability
• 1.0: Questions demonstrate perfect reliability and consistency
• Acceptable Threshold: Generally, reliability coefficients above 0.7 are considered acceptable for educational assessments

Mathematical Foundation

Cronbach’s Alpha Formula

The reliability coefficient shown is calculated using Cronbach’s Alpha (α):

α = (k/(k-1)) × (1 - (Σσ²ᵢ/σ²ₜ))

Where:

• k = number of questions/items in the test
• σ²ᵢ = variance of individual question scores
• σ²ₜ = variance of total test scores
• Σσ²ᵢ = sum of all individual question variances

Alternative Correlation-Based Formula

α = (k × r̄)/(1 + (k-1) × r̄)

Where:

• k = number of questions
• r̄ = average inter-item correlation

Technical Interpretation & Calculations

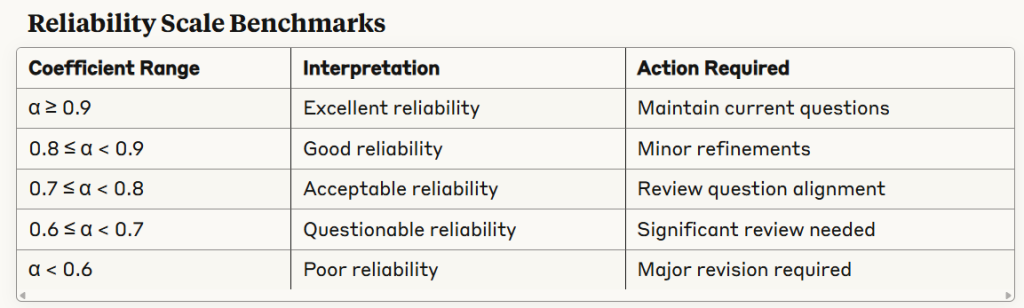
Chart Analysis with Calculations

Based on the displayed values:

ELA and Math: α ≈ 0.6

• Reliability Status: Questionable
• Measurement Error: SE = σ√(1-α) = σ√(1-0.6) = σ × 0.632
• Confidence: 60% of variance attributed to true score differences

Social Studies (SS): α ≈ 0.8

• Reliability Status: Good
• Measurement Error: SE = σ√(1-α) = σ√(1-0.8) = σ × 0.447
• Confidence: 80% of variance attributed to true score differences

Standard Error of Measurement (SEM)

SEM = σ × √(1 - α)

Practical Example: If a Math test has:

• Standard deviation (σ) = 15 points
• Reliability (α) = 0.6

Then: SEM = 15 × √(1 – 0.6) = 15 × 0.632 = 9.48 points

This means individual scores could vary by ±9.48 points due to measurement error alone.

Confidence Intervals for True Scores

True Score Range = Observed Score ± (Z × SEM)

For 95% confidence: Z = 1.96 For 68% confidence: Z = 1.00

Example: Student scores 75 on Math test (α = 0.6, σ = 15)

• SEM = 9.48
• 95% CI: 75 ± (1.96 × 9.48) = 56.4 to 93.6

Quality Improvement Calculations

Required Sample Size for Reliability Studies

n ≥ (Z²α/2 × (1-α)²)/(E² × α²)

Where E = acceptable margin of error

Item-Total Correlation Threshold

Questions should typically show correlations ≥ 0.3 with total score:

rᵢₜ = (rᵢₓ - rₜₓ × rᵢₜ)/√((1-r²ₜₓ)(1-r²ᵢₜ))

Practical Implications

Decision Matrix Based on Reliability Coefficients:

α ≥ 0.8 (Social Studies)

• Action: Maintain current question bank
• Confidence: High precision in student ability measurement
• Use Case: Suitable for high-stakes assessments

α = 0.6 (ELA, Math)

• Action: Review and enhance question alignment
• Confidence: Moderate precision, interpret scores cautiously
• Use Case: Acceptable for formative assessment, problematic for summative

This metric helps OnTarget users understand the measurement precision of their assessments and provides quantitative guidance for question bank optimization to improve testing reliability.