Question Difficulty Distribution – P-Value (Technical)

Definition

In psychometric analysis, the question difficulty p-value represents the proportion of test-takers who answered a question correctly. Unlike statistical hypothesis testing, this p-value ranges from 0.0 to 1.0 and serves as a direct measure of item difficulty.

Calculation Formula

The item difficulty p-value is calculated using the following formula:

P-value = (Number of correct responses) ÷ (Total number of responses)

Where:

• P-Value ranges from 0.00 to 1.00
• 0.00 = No one answered correctly (most difficult)
• 1.00 = Everyone answered correctly (easiest)

Example Calculations:

• If 75 out of 100 test-takers answer correctly: P-value = 75/100 = 0.75
• If 30 out of 100 test-takers answer correctly: P-value = 30/100 = 0.30
• If 95 out of 100 test-takers answer correctly: P-value = 95/100 = 0.95

Interpretation Scale

• P-value = 0.0: No test-takers answered correctly (extremely difficult)
• P-value = 0.5: 50% of test-takers answered correctly (moderate difficulty)
• P-value = 1.0: All test-takers answered correctly (extremely easy)

Distribution Analysis

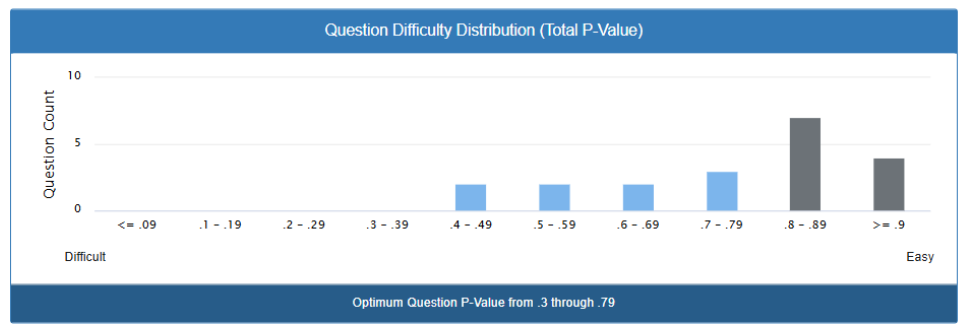
The screenshot displays a difficulty distribution histogram showing:

Difficulty Classification:

• ≤0.09: Extremely difficult questions (very few correct responses)
• 0.1-0.29: Difficult questions
• 0.3-0.49: Moderately difficult questions
• 0.5-0.69: Moderate difficulty questions
• 0.7-0.89: Easy questions
• ≥0.9: Very easy questions

Optimum Range Indicator: The highlighted section shows “Optimum Question P-Value from .3 through .79”, indicating the recommended difficulty range for effective assessment discrimination.

Observed Distribution Pattern:

The chart reveals a right-skewed distribution with:

• Peak concentration in the 0.8-0.89 range (~340 questions)
• Secondary peak at 0.7-0.79 range (~280 questions)
• Minimal questions in extremely difficult ranges (≤0.29)

Psychometric Significance

Optimal Difficulty Range (0.3-0.79):

• Provides maximum discrimination between high and low performers
• Ensures questions are neither too easy (ceiling effect) nor too difficult (floor effect)
• Supports reliable measurement across the ability spectrum

Distribution Quality Indicators:

• Balanced distribution: Questions spread across difficulty levels
• Concentration in optimal range: Most items fall within the 0.3-0.79 range
• Minimal extreme values: Few items at the very easy (>0.9) or very difficult (<0.3) extremes

Psychometric Rationale:

1. Discrimination Power: Questions with P-values between 0.3-0.7 typically provide maximum discrimination between high and low performers
2. Reliability: Items in this range contribute most effectively to test reliability
3. Information Function: These difficulty levels provide optimal measurement precision

Statistical Considerations:

Item Discrimination Formula:

Point-Biserial Correlation = (Mean score of correct group - Mean score of total group) / Standard deviation of total scores × √(p/(1-p))

Where optimal discrimination occurs when p ≈ 0.5, with acceptable ranges extending from 0.3-0.7.

Quality Implications

Current Distribution Assessment:

• Strength: Substantial number of questions (680+) in optimum range
• Concern: Heavy concentration in easy ranges (0.7-0.9) may indicate:
  • Insufficient challenge for higher-ability examinees
  • Potential ceiling effects
  • Reduced ability to differentiate among high performers

Recommendations:

1. Balance Enhancement: Increase proportion of questions in 0.3-0.6 range
2. Ceiling Effect Mitigation: Reduce over-concentration in 0.8+ ranges
3. Floor Effect Prevention: Maintain minimal presence of extremely difficult items (≤0.2)

Technical Applications

This P-value distribution data enables:

• Adaptive Testing: Item selection based on examinee ability estimates
• Test Equating: Maintaining consistent difficulty across test forms
• Content Validation: Ensuring appropriate cognitive demand distribution
• Performance Prediction: Estimating score distributions for planning purposes

The analysis suggests a test bank weighted toward easier items, which may be appropriate depending on the assessment’s purpose (certification vs. selection vs. diagnostic evaluation).